3d Range-Based Set Reconciliation
When two peers wish to synchronise data, they typically first exchange which Areas in which namespaces they are interested in. Intersecting these Areas yields the sets of Entries for which they then need to bring each other up to speed. In this document, we present a strategy for doing so efficiently.
Given the Entries that the peers have available, there can be two cases that necessitate data exchange. First, one peer might have an Entry that the other does not have, and second, the peers might hold nonequal parts of the Payload of some common Entry.
As a first step to solving the problem, we simplify it. If Entries contained information about locally available Payload bytes, then both cases would merge into a single case: one peer might have a datum that the other lacks. Hence, we do not synchronise Entries directly, but LengthyEntries:
struct LengthyEntryThe task of the two peers then becomes conceptually simple: they each have a set of LengthyEntries, and they need to inform each other about all LengthyEntries the other party does not have, that is, they each need to compute the union of their two sets. In the scientific literature, this problem is known as set reconciliation11Minsky, Yaron, Ari Trachtenberg, and Richard Zippel. "Set reconciliation with nearly optimal communication complexity." IEEE Transactions on Information Theory 49.9 (2003): 2213-2218..
Once the two peers have reconciled their sets, they can filter out Entries that overwrite each other, and they can separately request any missing (suffixes of) Payloads. Going forward, we thus concentrate on the set reconciliation part only.
To perform set reconciliation, we adapt the approach of range-based set reconciliation22Meyer, Aljoscha. "Range-Based Set Reconciliation." 2023 42nd International Symposium on Reliable Distributed Systems (SRDS). IEEE, 2023...
Range-based set reconciliation solves the problem recursively. To reconcile two sets, one peer first computes a hash over all items in its set, and sends this fingerprint to the other peer. That peer then computes the fingerprint over its items as well. If the fingerprints match, they are done reconciling.

If they do not match, there are two options. First, the peer can split its set in half and then initiate set reconciliation for each half concurrently (by transmitting its hashes for both halves). Second, if the set is sufficiently small, the peer can instead simply transmit its items in the set. The other peer responds to this with all other items that it held in the set, completing the process of reconciliation.
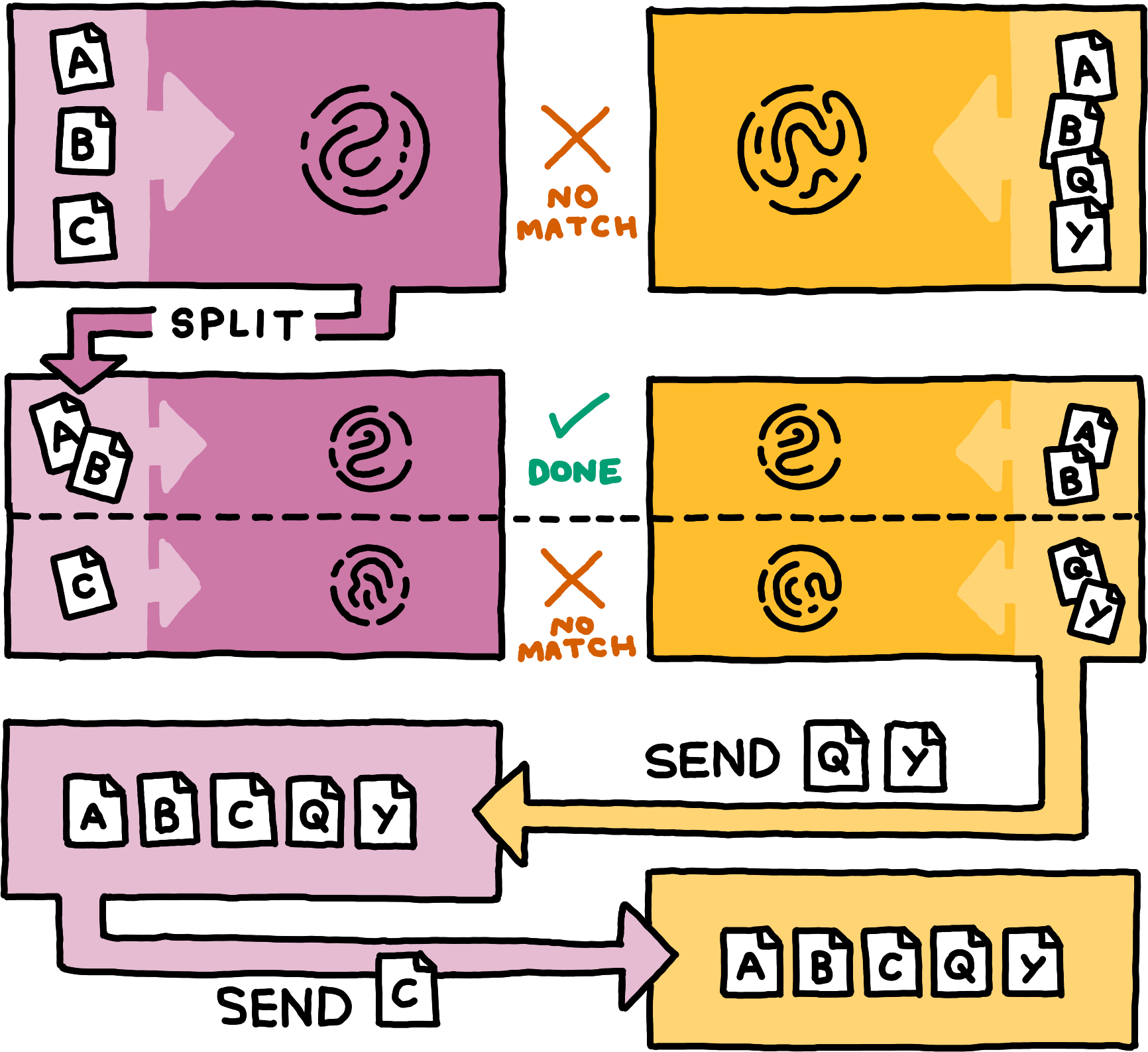
A and B, and another 3dRange including C, and sends these 3dRanges and their fingerprints to Betty. Betty produces a matching fingerprint for the first 3dRange. As the other, mismatched 3dRange includes so few Entries, Betty sends her Entries Q and Y to Alfie. In response, Alfie sends Entry C to Betty.Overall, the peers collaboratively drill down to the differences between their two sets in a logarithmic number of communication rounds, spending only little bandwidth on those regions of the original sets where they hold the same items. Note that peers can actually split sets into arbitrarily many subsets in each step. Splitting into more subsets per step decreases the total number of communication rounds.
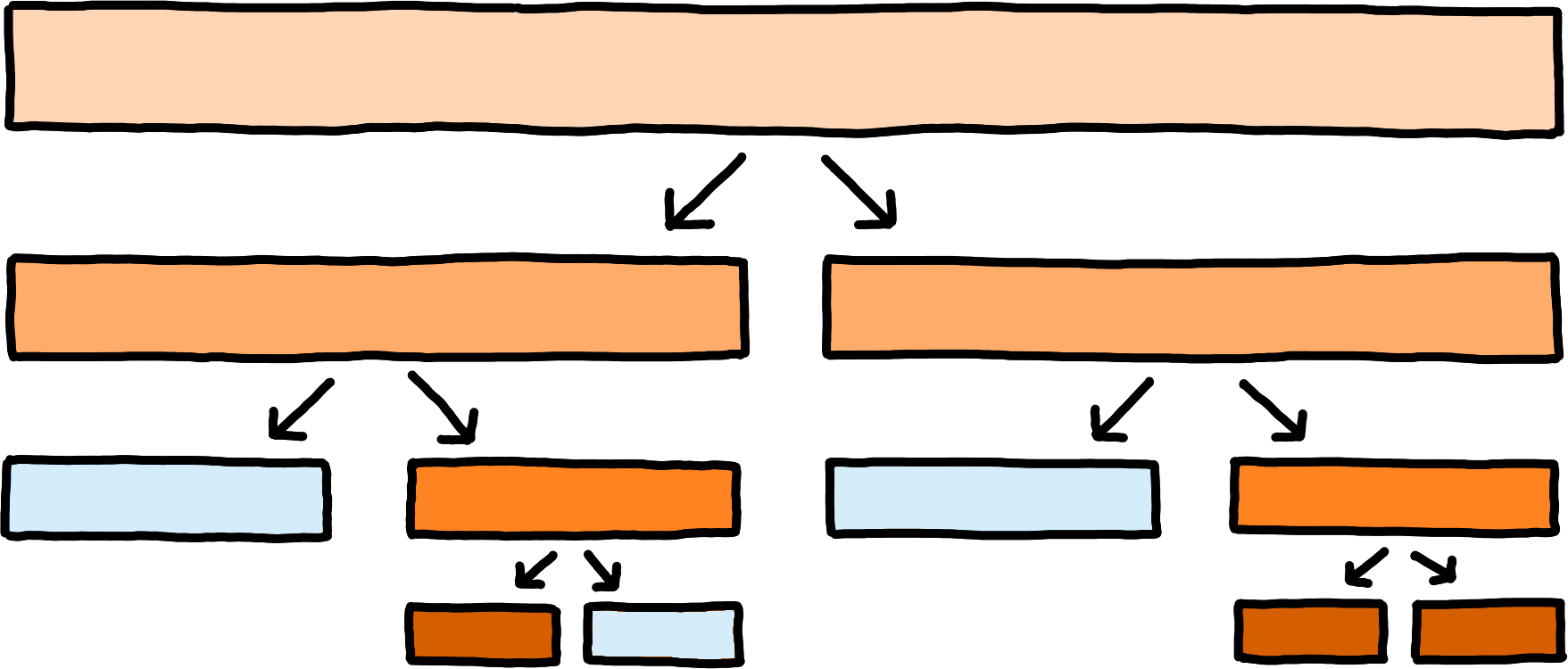
3d range-based set reconciliation takes these ideas and applies them to Willow. The core design decision is to delimit sets of LengthyEntries via 3dRanges. When a peer splits its 3dRanges, it is crucial for overall efficiency to not split based on volume (for example, by splitting the times in half numerically), but to split into subranges in which the peer holds roughly the same number of Entries.
Let Fingerprint denote the type of hashes of LengthyEntries that the peers exchange. Then the precise pieces of information that the peers need to exchange are the following:
struct 3dRangeFingerprintThe 3dRange in question.The set of LengthyEntries a peer holds in some 3dRange.struct 3dRangeEntrySetThe 3dRange in question.The LengthyEntries that the sender holds in the 3d_range.A boolean flag to indicate whether the sender wishes to receive the other peer’s 3dRangeEntrySet for the same 3d_range in return.To initiate reconciliation of a 3dRange, a peer sends its 3dRangeFingerprint. Upon receiving a 3dRangeFingerprint, a peer computes the Fingerprint over its local LengthyEntries in the same range.
If it does not match, the peer either sends a number of 3dRangeFingerprints whose 3dRanges cover the 3dRange for which it received the mismatching Fingerprint. Or it replies with its 3dRangeEntrySet for that 3dRange, with the want_response flag set to true.
To any such 3dRangeEntrySet, a peer replies with its own 3dRangeEntrySet, setting the want_response flag to false, and omitting all LengthyEntries it had just received in the other peer’s 3dRangeEntrySet.
When a peer receives a 3dRangeFingerprint that matches the Fingerprint over its local LengthyEntries in the same 3dRange, the peer should reply with an empty 3dRangeEntrySet for that 3dRange, setting the want_response flag to false. This notifies the sender of the 3dRangeFingerprint that reconciliation has successfully concluded for the 3dRange.
The peers might be interested in when they have successfully reconciled a particular 3dRange. Unfortunately, tracking all the 3dRanges that you receive and determining whether their union covers the particular 3dRange you are interested in is a comparatively expensive (and annoying) algorithmic problem. To circumvent this problem, peers can attach small bits of metadata to their messages: whenever a peer splits a 3dRange into a set of covering 3dRanges, the peer can simply attach some metadata to the final such subrange that it sends that indicates which of the 3dRanges sent by the other peer has now been fully covered by subranges.
As long as both peers are accurate in supplying this metadata, they can maintain perfect information about the progress of reconciliation without the need for any sophisticated data structures. Peers should be cautious that a malicious peer could provide wildly inadequate metadata, but in general this is tolerable: a malicious peer can sabotage reconciliation in all sorts of interesting ways regardless.
Fingerprinting
3d range-based set reconciliation requires the ability to hash arbitrary sets of LengthyEntries into values of some type Fingerprint. To quickly compute Fingerprints, it helps if the Fingerprint for a 3dRange can be assembled from precomputed Fingerprints of other, smaller 3dRanges. For this reason, we define the fingerprinting function in terms of some building blocks: LengthyEntries are mapped into a set PreFingerprint with a function that satisfies certain algebraic properties that allow for incremental computation, and PreFingerprints are then convertedThe split into PreFingerprints and Fingerprints allows for compression: the PreFingerprints might be efficient to compute but rather large, so you would not want to exchange them over the network. Converting a PreFingerprint into a Fingerprint can be as simple as hashing it with a typical, secure hash function, thus preserving collision resistance but yielding smaller final fingerprints. into the final Fingerprint.
First, we require a function fingerprint_singleton that hashes individual LengthyEntries into the set PreFingerprint. This hash function should take into account all aspects of the LengthyEntry: modifying its namespace_id, subspace_id, path, timestamp, payload_digest, payload_length, or its number of available bytes, should result in a completely different PreFingerprint.
Second, we require an associative and commutative33Classic range-based set reconciliation does not require commutativity. We require it because we do not wish to prescribe how to linearise three-dimensional data into a single order. function fingerprint_combine that maps two PreFingerprints to a single new PreFingerprint. The fingerprint_combine function must further have a neutral element fingerprint_neutral.
Third, we require a function fingerprint_finalise that maps each PreFingerprint into the corresponding Fingerprint.
| Set | Fingerprint |
|---|---|
| { } |  | {  } } |  | {    } } |  |
Given these building blocks, we define the function fingerprint from sets of LengthyEntries to Fingerprint:
- applying fingerprint to the empty set yields fingerprint_finalise(fingerprint_neutral),
- applying fingerprint to a set containing exactly one LengthyEntry yields the same result as applying fingerprint_singleton to that LengthyEntry and then applying fingerprint_finalise, and
- applying fingerprint to any other set of LengthyEntries yields the result of applying fingerprint_singleton to all members of the set individually, then combining the resulting Fingerprints with fingerprint_combine (grouping and ordering do not matter because of associativity and commutativity), and then applying fingerprint_finalise.
For 3d range-based set reconciliation to work correctly, fingerprint must map distinct sets of LengthyEntries to distinct Fingerprints with high probability, even when facing maliciously crafted input sets. The range-based set reconciliation paper surveys suitable, cryptographically secure hash functions in section 5B. All but the Cayley hashes use commutative fingerprint_combine functions, and are thus suitable for 3d range-based set reconciliation. Further, fingerprint_finalise must not map distinct inpus to equal outpts; suitable choices are the identity function (if no compression is needed) or traditional, secure hash functions.