Read Access and Confidentiality

  1. Setting and Goals
    1. Techniques Overview
      1. All the Details
        1. Private Interests
          1. Private Overlap
            1. Examples and proof sketches
            2. Exchanging Capabilities
              1. Awkwardness
              2. Security Properties
                1. Threat Model
                  1. Scope
                    1. Goals
                      1. Muriarty
                        1. Epson
                      2. Meadowcap Enumeration Capabilities
                        1. References

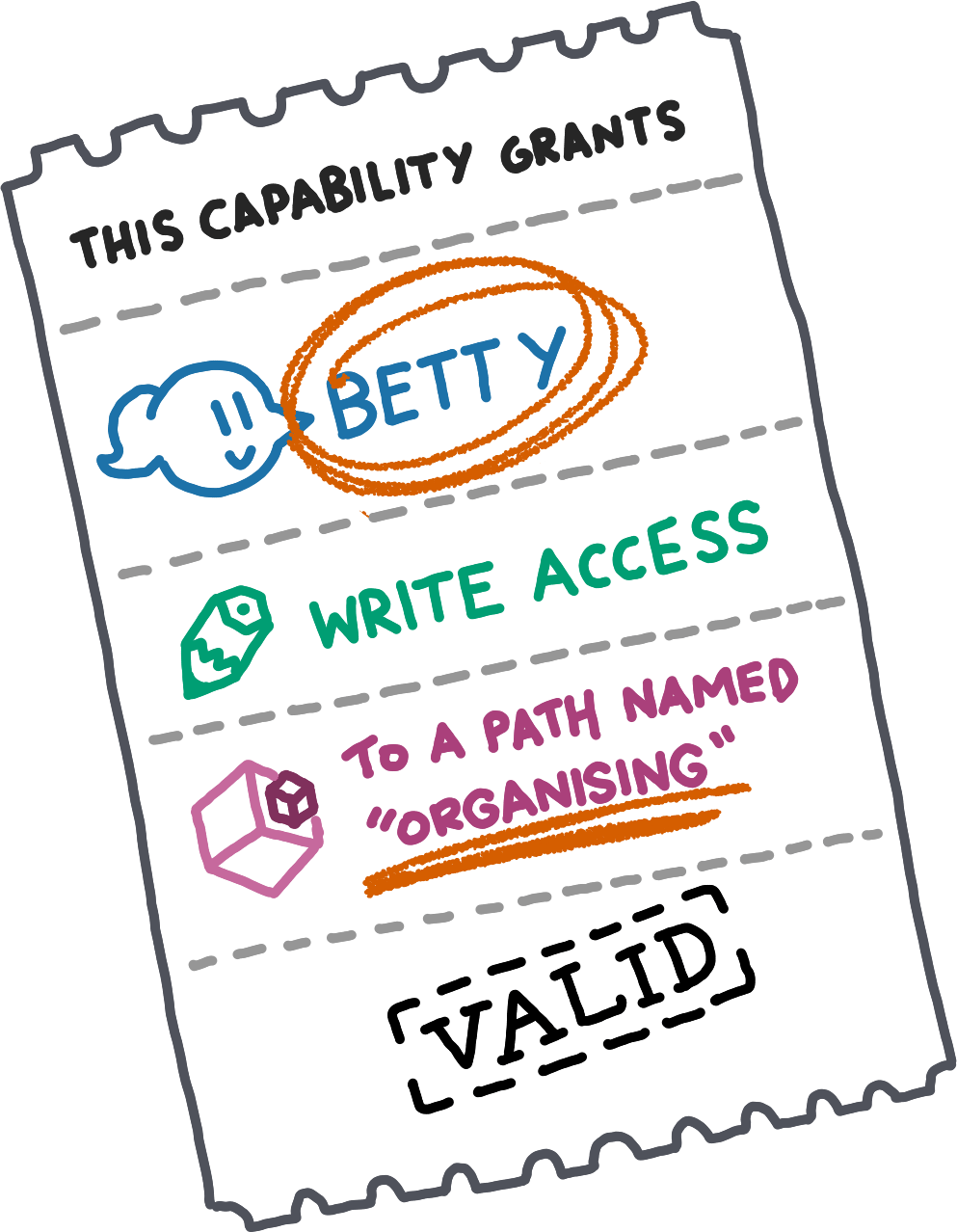                          A ticket representing a capability, detailing the capability's receiver (Betty), and that it grants write access to a path named 'organising'. Someone has circled these details messily with a red marker.This document details a mechanism for implementing capability-enforced read-access-control when synchronising data between two Willow peers. This is more complex than simply defining a type of read access capabilities and then exchanging those in the open, because such a process would leak information such as NamespaceIds, SubspaceIds, and Paths to peers without read-access. We describe a more sophisticated technique that does not leak such information, even in realistic adversarial settings.

                          Setting and Goals

                          We want to allow peers to specify pairs of namespaces and AreasOfInterest, and then synchronise the intersections. Furthermore, a peer should only be given access to information for which it can prove that the original author allows them to access it. To this end, we start by defining the notion of a read capability.

                          A read capability is an unforgeable token that grants read access to some data to the holder of some secret key. More formally, a read capability must be a piece of data for which three types of semantics are defined:Meadowcap, our bespoke capability system for Willow, just so happens to provide these semantics with its McCapabilities of access mode read.

                          Access control can then be implemented by answering only requests for Entries in the granted namespace and granted area of some read capability whose receiver is the peer in question.

                          The simplemost solution consists in the peers openly exchanging read capabilities and then specifying their AreasOfInterest, which must be fully included in the granted areas of the read capabilities. This works well for managing read access control and determining which Entries to synchronise, but it leaks some potentially sensitive information. Two examples:

                          First, suppose that Alfie creates an Entry at Path gemma_stinks, and gives a read capability for this Path to Betty. Later, Betty connects to Gemma's machine for syncing, and asks for gemma_stinks in Alfie’s subspace. In sending her read capability, she hands a signed proof to Gemma that Alfie thinks1,21Gemma does not, in fact, stink.2Also, Alfie is really very nice and would never say such a thing outside of thought experiments for demonstrating the dangers of leaking Paths. she stinks. Not good.

                          Second, suppose a scenario where everyone uses encrypted paths, with individual encryption keys per subspace. Alfie synchronises with Betty, asking her for random-looking Paths of the same structure in ten different subspaces. Betty has the decryption keys for all but one of the subspaces. All the paths she can decrypt happen to decrypt to gemma_stinks. This gives Betty a strong idea about what the tenth person thinks of Gemma, despite the fact that Betty cannot decrypt the Path. Not good.

                          Ideally, we would like to employ a mechanism where peers cannot learn any information beyond the granted areas of the read capabilities which they hold at the start of the process. Unfortunately, such a mechanism would have to involve privacy-preserving verification of cryptographic signatures, and any suitable primitives are exceedingly complicated.

                          Instead, we design solutions which do not allow peers to learn about the existence of any NamespaceId, SubspaceId, or Path which they did not know about already. If, for example, both peers knew about a certain namespace, they should both get to know that the other peer also knows about that namespace. But for a namespace which only one of the peers knows about, the other peer should not learn its NamespaceId.

                          Such solutions cannot prevent peers from confirming guesses about data they shouldn't know about. Hence, it is important that NamespaceIds and SubspaceIds are sufficiently long and random-looking. Similarly, encrypting Components with different encryption keys for different subspaces can ensure that Paths are unguessable. Because valid TimestampsFinding efficient encryption schemes and privacy-preserving synchronisation techniques that work for Timestamps is an interesting research endeavour, but out of scope for us. can easily be guessed, we do not try to hide information about them.

                          In addition to withholding information from unauthorised peers, we also wish to defend against active eavesdroppers. An active eavesdropper is an attacker who can read and modify all transmissions by the two peers. There exist well-known protections for settings where the two peers have prior knowledge about each other before they start the connection, but we also want to allow for sync between anonymous peers who do not know each other at all. Hence, even after the other peer has proven to us that they have access to some data, we still must be careful about what we send (or rather, how we encrypt it).

                          Techniques Overview

                          At a high level, we employ three mechanism for preserving Entry confidentiality:

                          • peers demand a proof that their sync partner is the receiver of a read capability before handing over data,
                          • communication sessions are encrypted such that they can only be decrypted by the receiver of the read capabilities, and
                          • peers exchange (salted) hashes of Areas instead of the Areas themselves.

                          The first bullet point should be straightforward: no requested data is explicitly handed over, unless the sync partner demonstrates that it was granted read access.

                          The second bullet point serves to defend against active eavesdroppers. At the start of the sync session, the two peers perform a handshake in which they negotiate how to encrypt their communication. A typical choice would be a Diffie–Hellman key exchange, which results in a shared secret, which can be used as the shared key for symmetric encryption of the communication session. Crucially, as part of the handshake, the peers prove to each other knowledge of the secret key corresponding to some public key they transmit. We require those to be public keys and secret keys for the signature scheme that denotes the receivers of read capabilities33All read capabilities that a single peer presents in a sync session must have the same receiver. This is not a restriction in practice when capabilities can be delegated. Peers can even create ephemeral keypairs per sync session and create valid capabilities by delegation which they discard after the session.. The peers only accept read capabilities whose receiver is the public key for which the other other peer proved it has the corresponding secret key.

                          An active eavesdropper faces a dilemma: if they do not manipulate the handshake, they cannot derive the decryption secret and cannot listen in on the sync session. If they do manipulate the handshake by replacing the exchanged public keys with ones for which they have the corresponding secret keys, then they will later have to produce read capabilities for those public keys. Since a good capability system makes forgery impossible, they will not be able to do so. The peers, then, will not transmit any sensitive data.

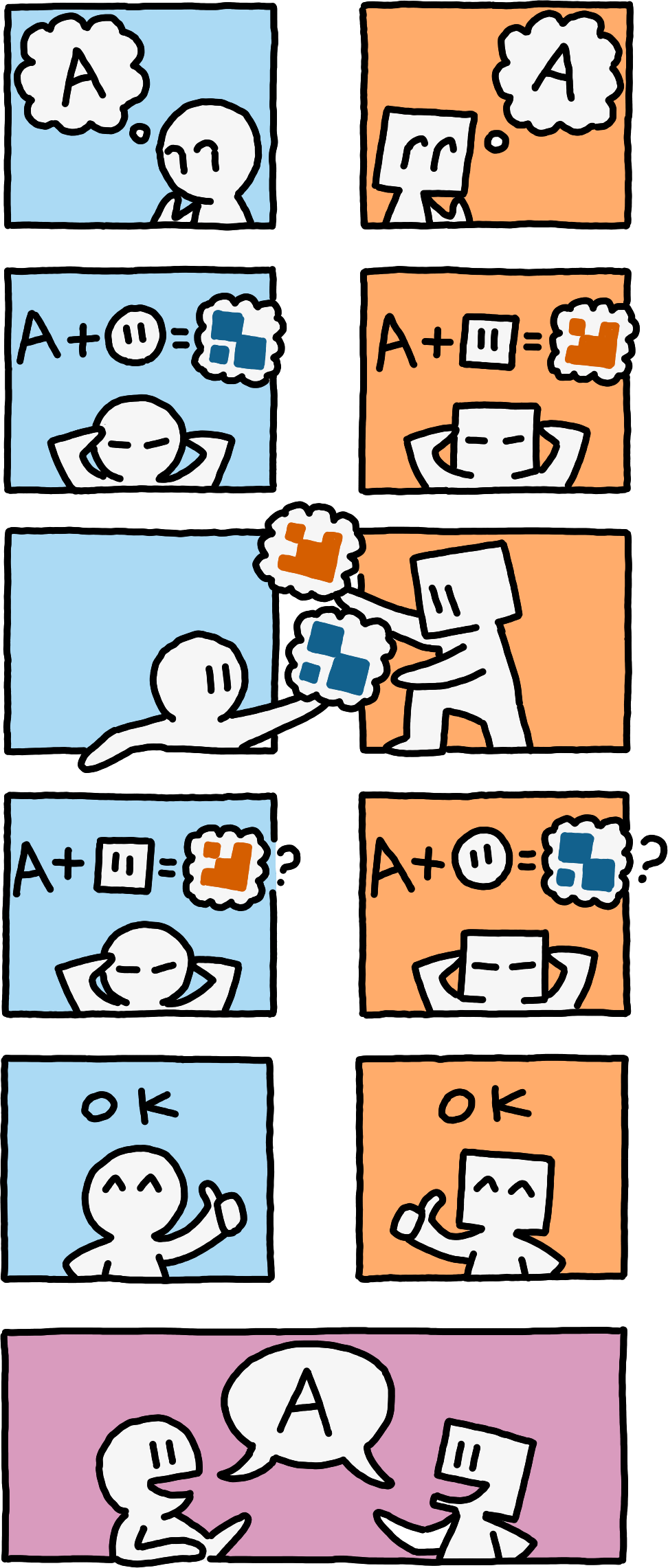                          A comic showing two characters creating hashes of a common piece of information using their own salt. When they receive each others' hashes, they compare it with a hash generated using their partner's salt.Telling a peer directly about which Areas in which namespaces you are interested in leaks NamespaceIds, SubspaceIds, and Paths. Instead, the peers merely transmit secure hashes of certain combinations of these. Intuitively, if both peers send the same hash, then they both know that they are interested in the same things. This is easily attackable however: one peer can simply mirror back hashes sent by the other, tricking them into beleaving that they have shared knowledge. For this reason, each peer is assigned a random bitstring to use as a salt for the hash function. A peer transmits hashes salted with its own salt, but compares the hashes it receives against hashes that it computes locally with the other peer’s salt.

                          Before we go into the details of which data precisely to hash, we want to point out that peers must use references to the common hashes instead of mentioning the underlying NamespaceIds, SubspaceIds, and Paths. In particular, when transmitting read capabilities, peers must encode them in a special format that omits the confidential data.

                          All the Details

                          We now switch from the preceding informational style to a more precise specification of how one can sync Willow data with untrusted peers while keeping most metadata confidential.

                          We shall assume that the connection between the two syncing peers is established via a handshake. We refer to the two peers as the initiator and the responder respectively to break symmetry. We require the handshake to have the following properties:These properties are more or less the bread-and-butter properties of authenticated Diffie-Hellman key exchanges; the noise framework XX handshake, for example, fulfils them.

                          • all communication over the connection after the handshake is encrypted, using a symmetric key known two both participants of the handshake,
                          • the symmetric key depends to some degree on two inputs ini_pk and res_pk, which are public keys submitted by the initiator and the responder respectively,
                          • during the handshake, the peers prove to each other knowledge of the respective secret keys for initiator and responder, and
                          • the two peers arrive at a random bytestringIn the noise framework, this corresponds to the GetHandshakeHash() function. rnd which cannot be dictated by any one peer alone.

                          Peers must reject any read capabilities presented to them whose receiver is not the ini_pk or res_pk respectively. This ensures that the information they exchange can only be decrypted by the receiver of the capabilities.

                          The rnd bytestring forms the basis for the two peers to salt their hashes. We define ini_salt as equal to rnd, and res_salt as the bytestring obtained by flipping every bit of rnd.

                          Private Interests

                          A ticket representing a capability, detailing the capability's receiver (Betty), and that it grants write access to a path named 'organising'. Someone has circled these details messily with a red marker.Before we go into further details, we introduce some compact terminology around the data we want to keep confidential (NamespaceIds, SubspaceIds, and Paths), starting by giving such triplets a name:

                          Confidential data that relates to determining the AreasOfInterest that peers might be interested in synchronising.
                           
                          any denotes interest in all subspaces of the namespace.
                          }

                          Let p1 and p2 be PrivateInterests.

                          We say p1 is more specific than p2 if

                          We say that p1 is strictly more specific than p2 if p1 is more specific than p2 and they are not equal.

                          We say that p1 is less specific than p2 if p2 is more specific than p1.

                          We say that p1 and p2 are comparable if p1 is more specific than p2or p2 is more specific than p1.

                          We say that p1 includes an Entry e if

                          We say that p1 and p2 are disjoint there can be no Entry which is included in both p1 and p2.

                          We say that p1 and p2 are awkward if they are neither comparable nor disjoint. This is the case if and only if one of them has subspace_id any and a path p, and the other has a non-any subspace_id and a path which is a strict prefix of p.

                          We say that p1 includes an Area a if

                          If p1 has a subspace_id that is not any, then we call the PrivateInterest that is equal to p1 except its subspace_id is any the relaxation of p1.

                          Private Interest Overlap

                          Peers want to find the non-empty intersections of their AreasOfInterest. We reduce this to first finding their non-disjoint PrivateInterests, and assume that TimeRanges and AreaOfInterest limitsCombining confidential PrivateInterest information with limits and TimeRanges in the clear might allow malicious peers to track correlations. We choose to err on the side of caution here. will be taken into consideration in a separate, later stage. The challenge then becomes to find overlapping PrivateInterests by comparing only small numbers of salted hashes. We assume there is a secure hash function h that maps pairs of salts (bytestrings) and PrivateInterests to bytestrings of some fixed width.

                          Explaining in advance how this solution came about is a bit difficult. So we are simply going to define it, and then argue that it is correct, without any real explanation. If that leaves you unhappy, you can at least take comfort in the fact that you did not have to come up with the solution yourself.For reasons that will become apparent later (spoiler: awkward PrivateInterests deserve their name), the peers exchange pairs of a salted hash and a boolean each, according to the following rules:

                          The boolean, in other words, is true if the hash corresponds to a PrivateInterest that the sending peer is actually interested in, and false if the hash corresponds merely to a relaxation that must be sent for technical reasons.

                          Each peer locally computes some further pairs of salted hashes and booleans: the computations follow the same rules as for sending, except that

                          Whenever a peer receives a hash-boolean pair, it compares it against its locally computed pairs. If it locally computed a pair with the same hash, and at least one of the two pairs has a boolean value of true, then the peer knows that there is an overlap between its own PrivateInterest that resulted in the matching pair and some PrivateInterest of the other peer. For each of its PrivateInterests that did not give rise to any matching pair, the peer knows it to be disjoint from all PrivateInterests of the other peer.

                          Examples and proof sketches

                          The following examples show which data the peers compute and exchange in various situations. We assume the NamespaceId to always be equal for both peers (all involved hashes will trivially be distinct for PrivateInterests of distinct namespace_ids) and omit them.

                          If you replace the concrete examples with the equivalence classes that they represent, you obtain a proof sketch for the correctness of this approach.The examples cover the nine different (up to symmetry) combinations of how subspace_ids and paths can related to each other (equal, non-equal, or any for subspace_ids, prefix, extension, or unrelated for paths). Note that in all examples, both peers also locally compute hashes for PrivateInterests with the empty Path. For brevity we do not depict those, since in these examples they never match any transmitted hashes.

                          Left: Gemma subspace, path a
                          Right: Gemma subspace, path a
                          The PrivateInterests are not disjoint. Both peers detect an overlap.
                          Left: any subspace, path a
                          Right: any subspace, path b
                          The PrivateInterests are disjoint. None of the hashes match.
                          Left: any subspace, path a
                          Right: any subspace, path ab
                          The PrivateInterests are not disjoint. The right peer detects an overlap.
                          Left: any subspace, path a
                          Right: Gemma subspace, path b
                          The PrivateInterests are disjoint. None of the hashes match.
                          Left: any subspace, path a
                          Right: Gemma subspace, path a
                          The PrivateInterests are not disjoint. This is a special case where both peers detect the overlap.
                          Left: any subspace, path a
                          Right: Gemma subspace, path ab
                          The PrivateInterests are not disjoint. The right peer detects an overlap.
                          Left: any subspace, path ab
                          Right: Gemma subspace, path a
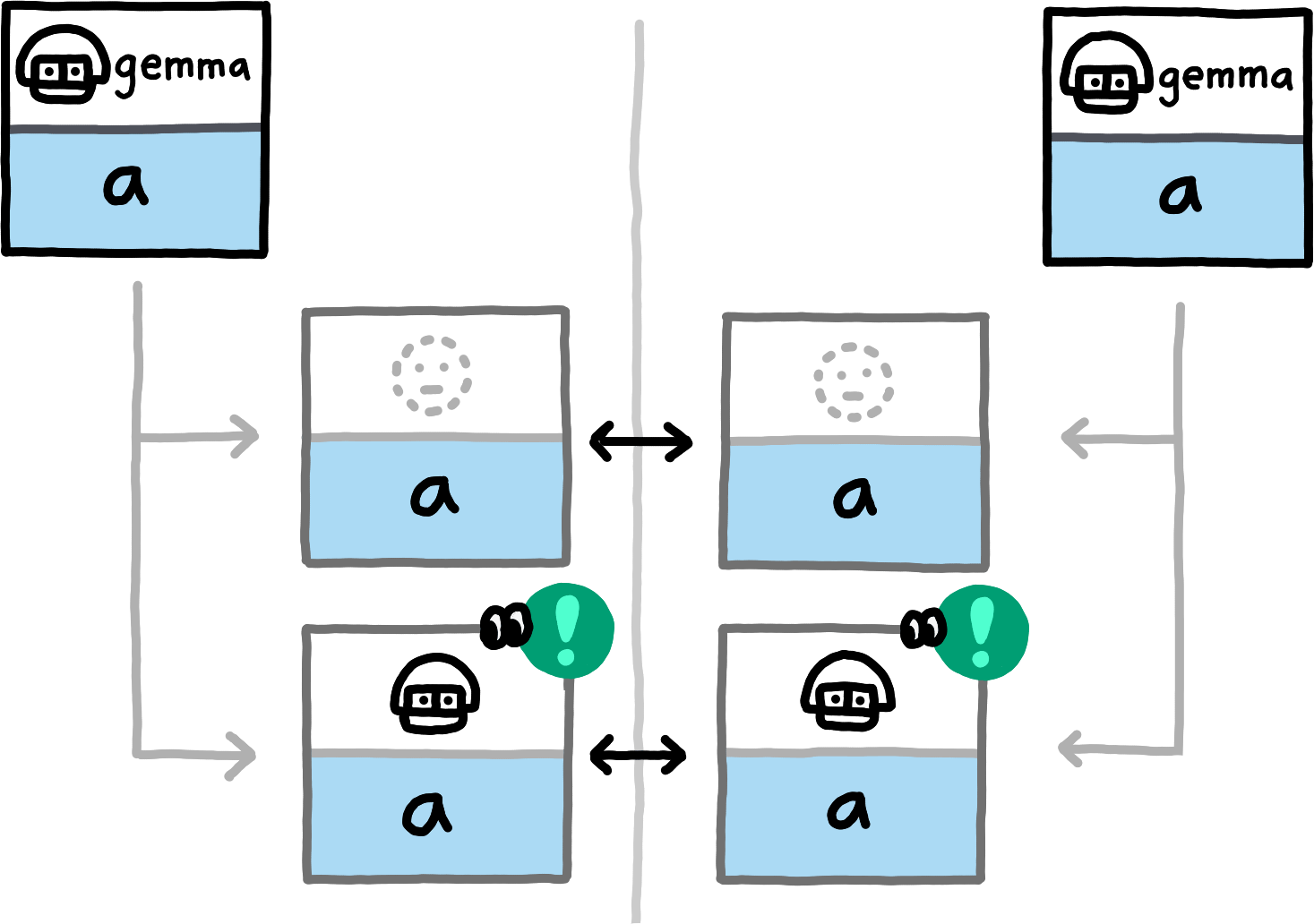
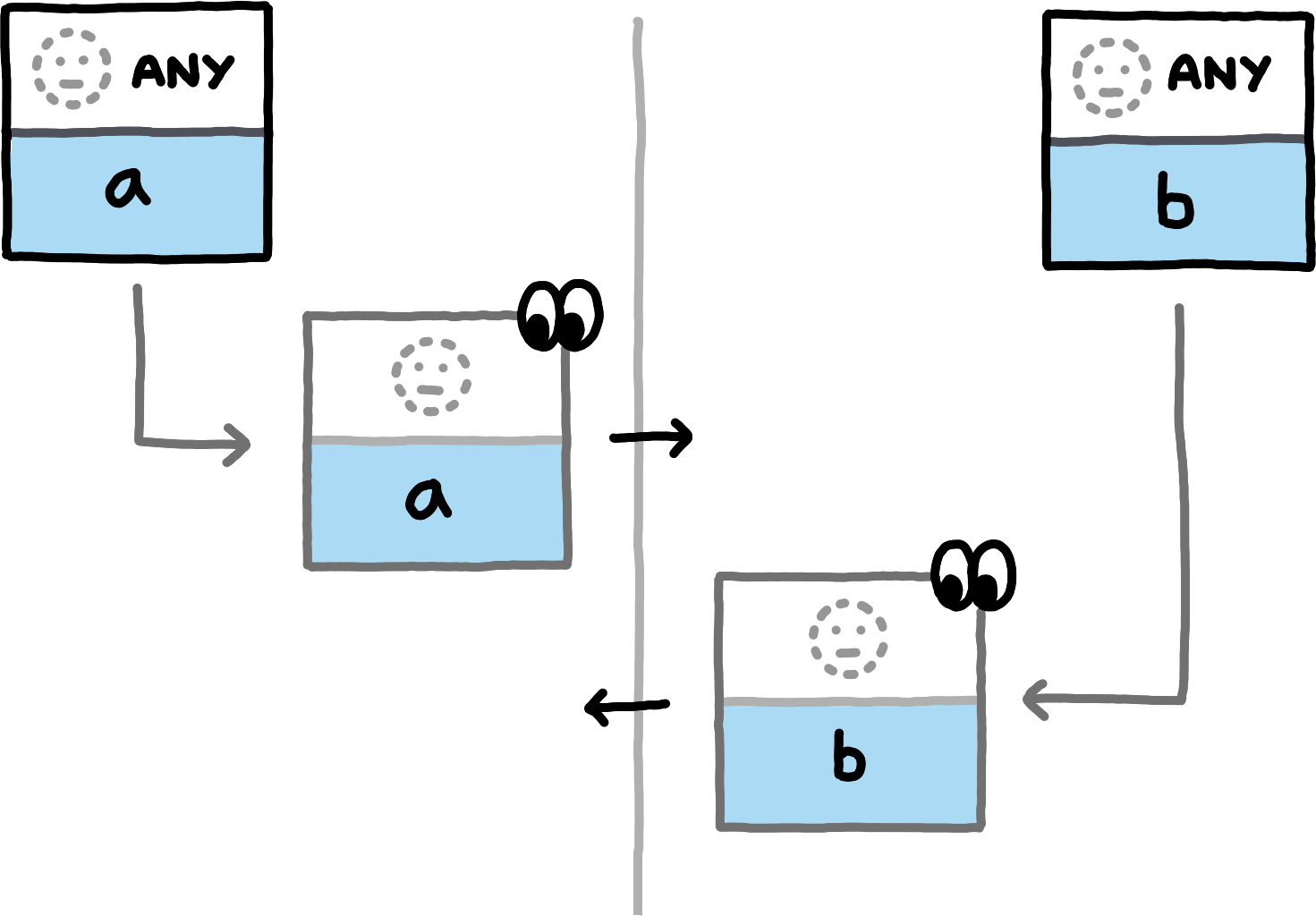
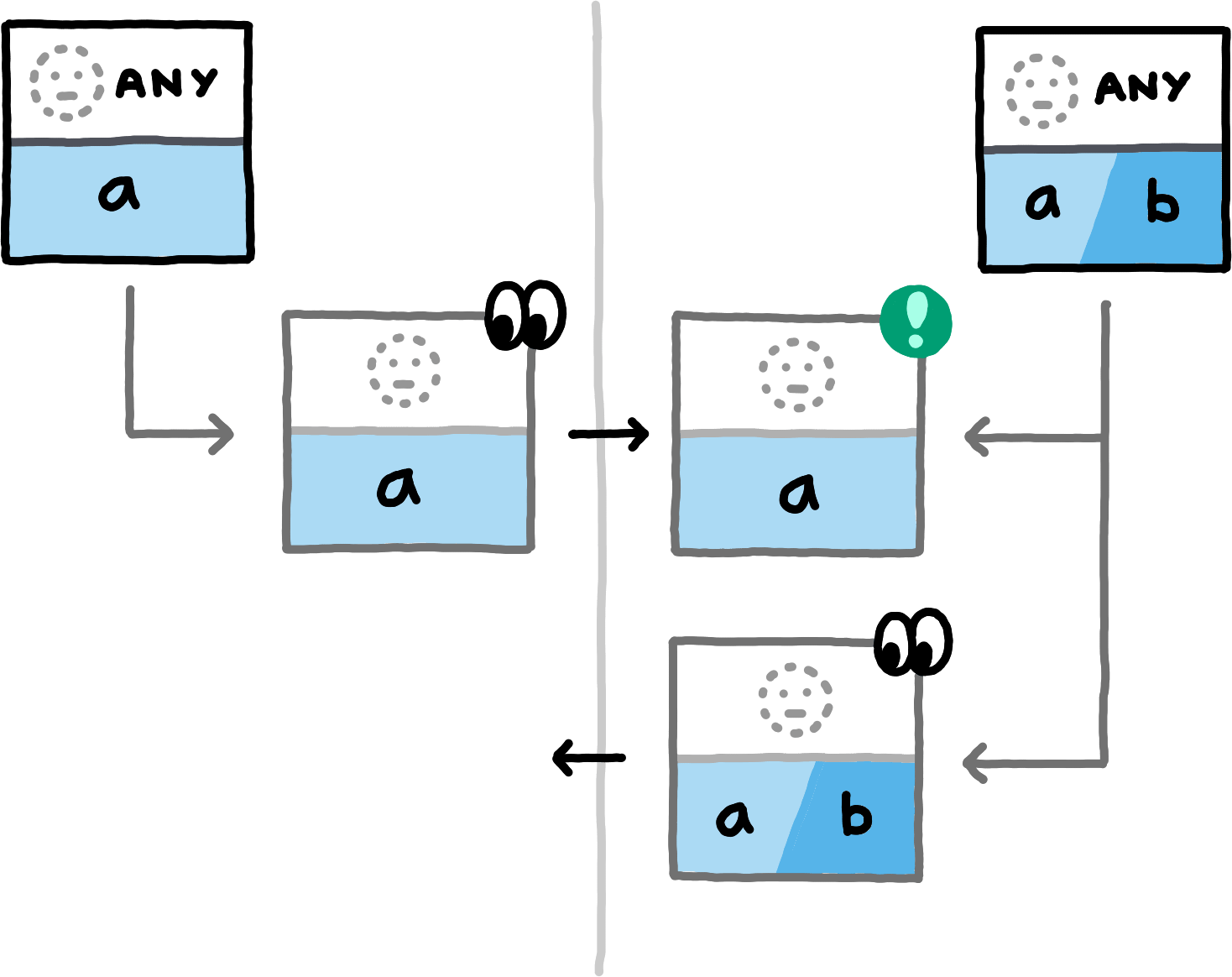
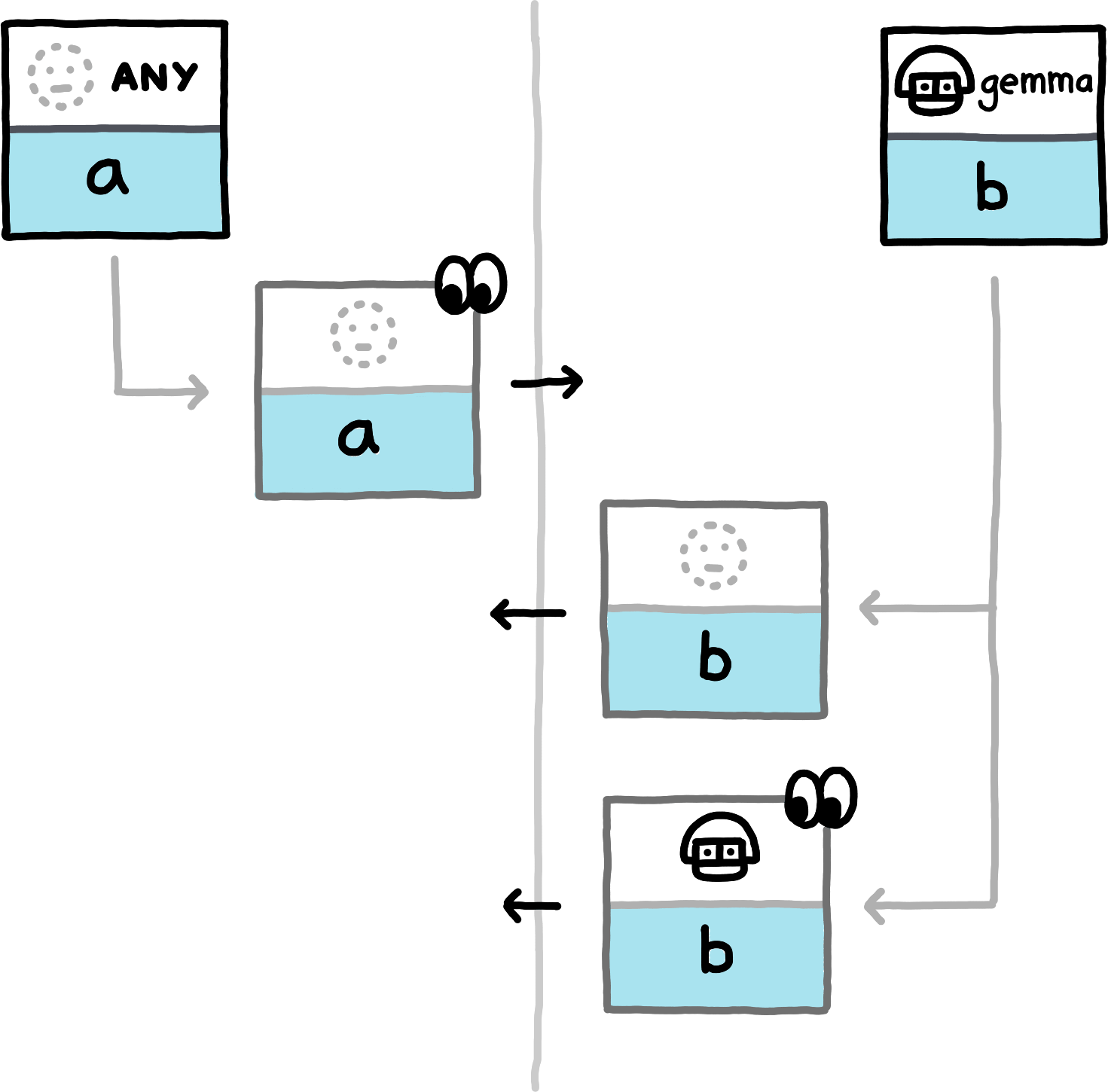
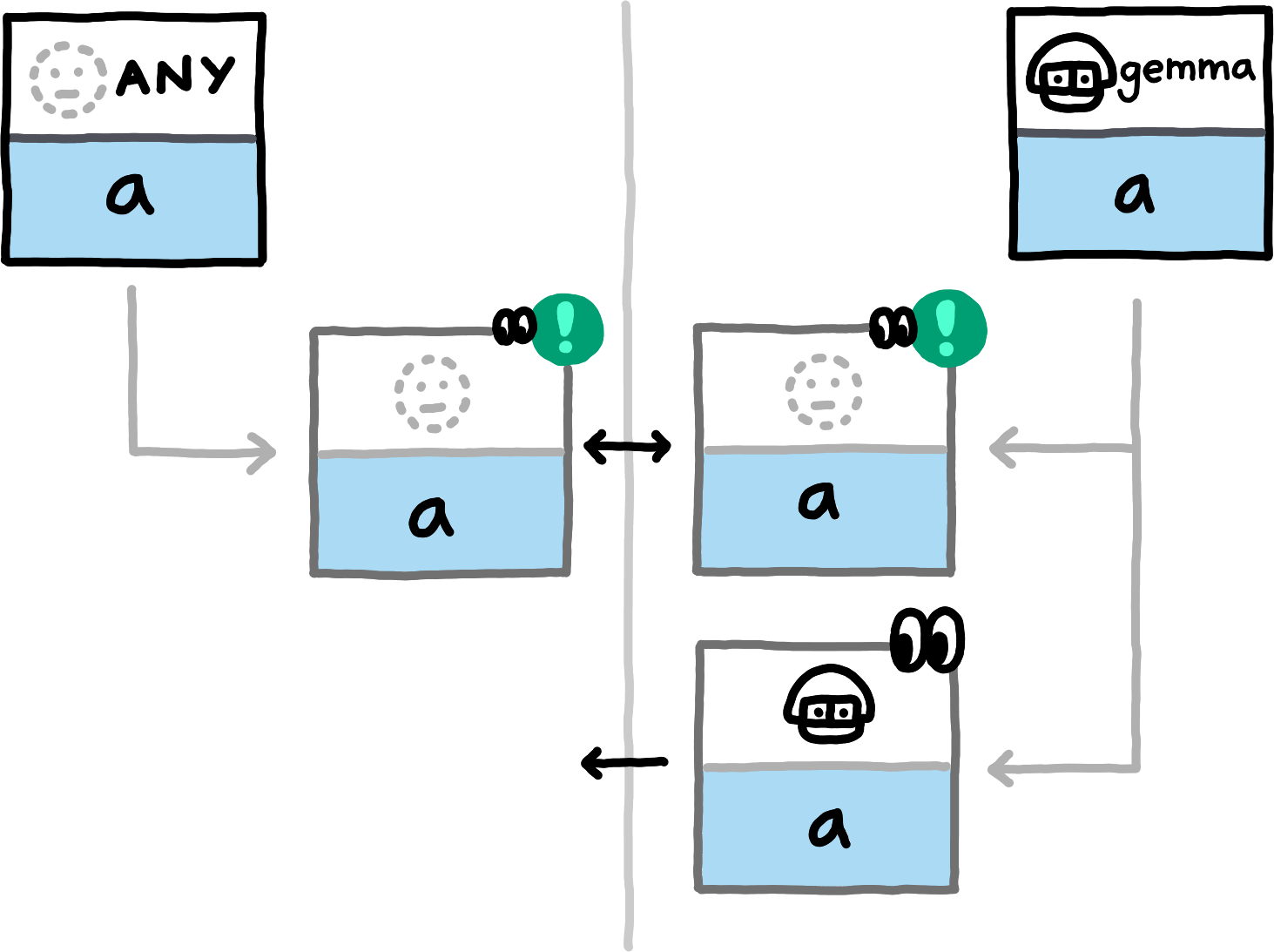
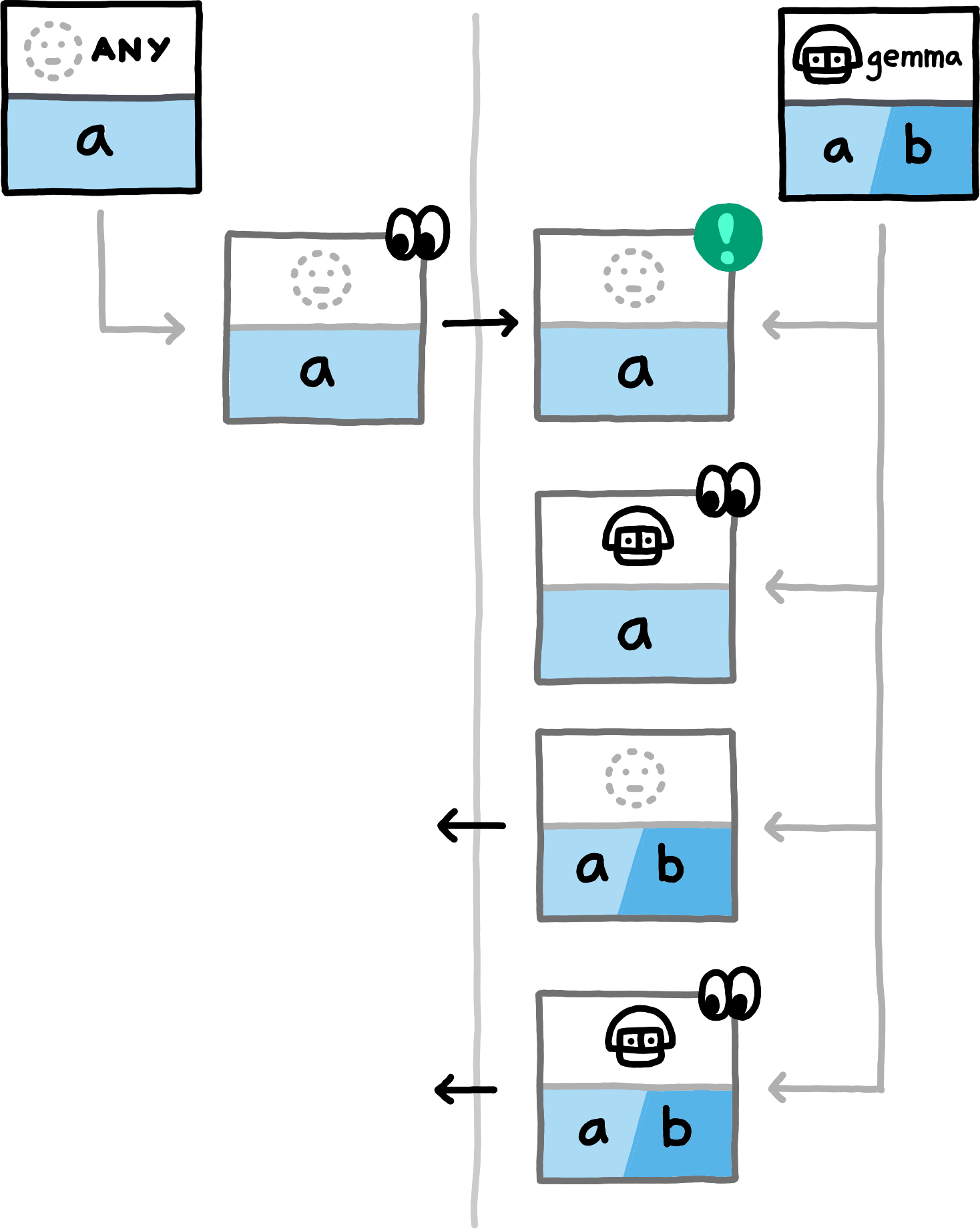
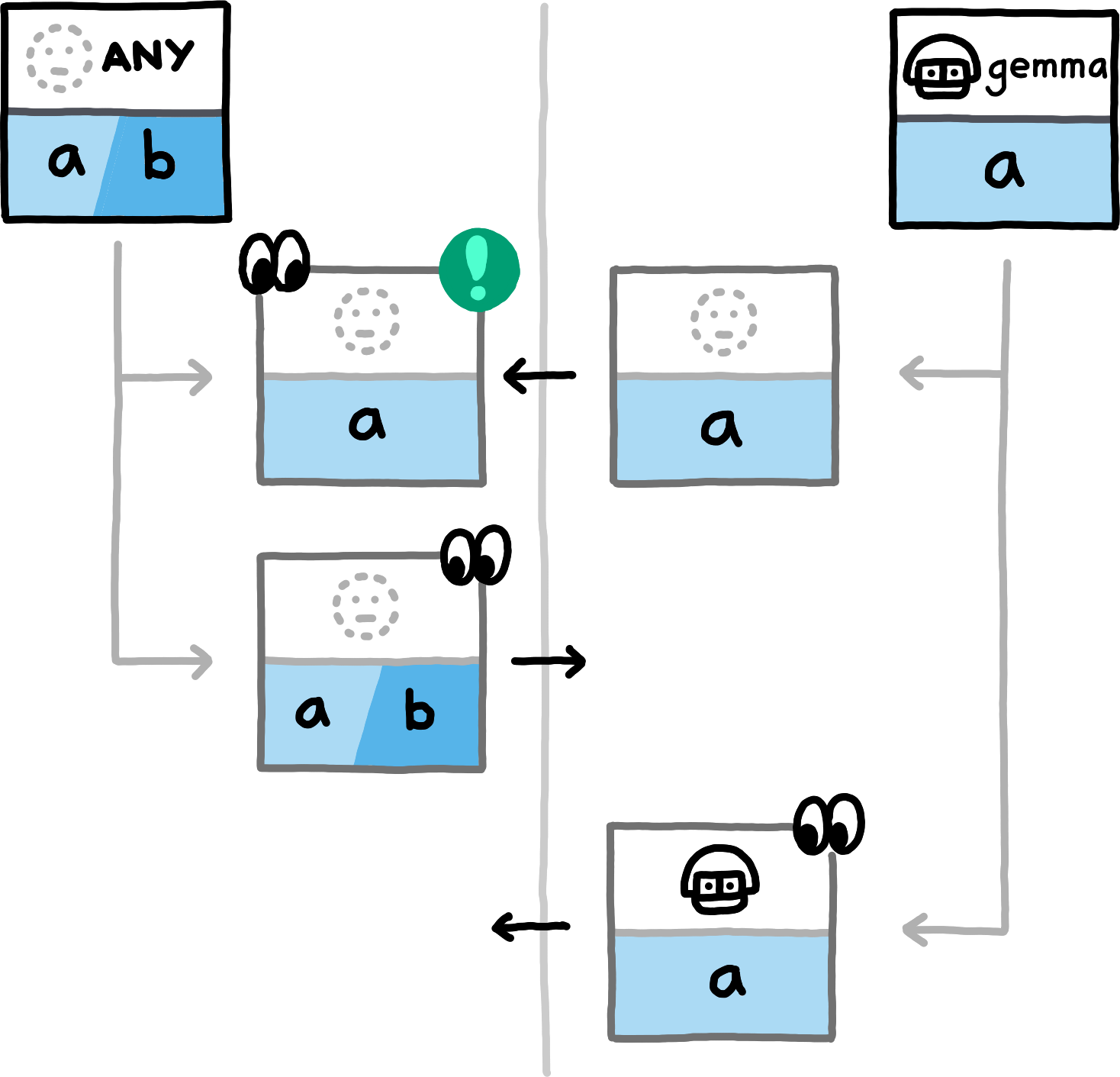
                          The PrivateInterests are not disjoint. The left peer detects an overlap. This example represents the case of awkward PrivateInterests; this is the only case in which a transmitted hash-boolean pair with a boolean of false is involved in detecting an overlap.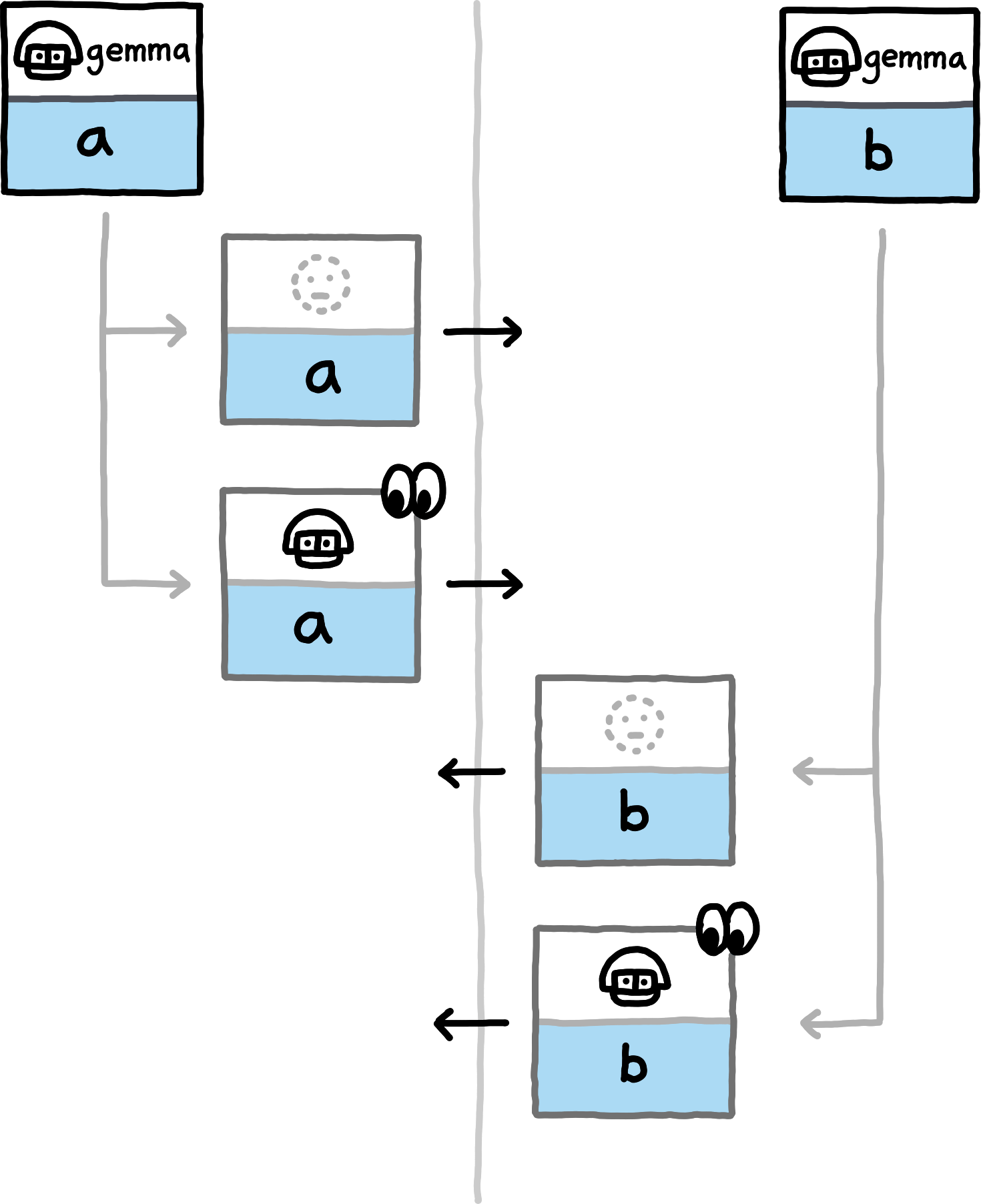
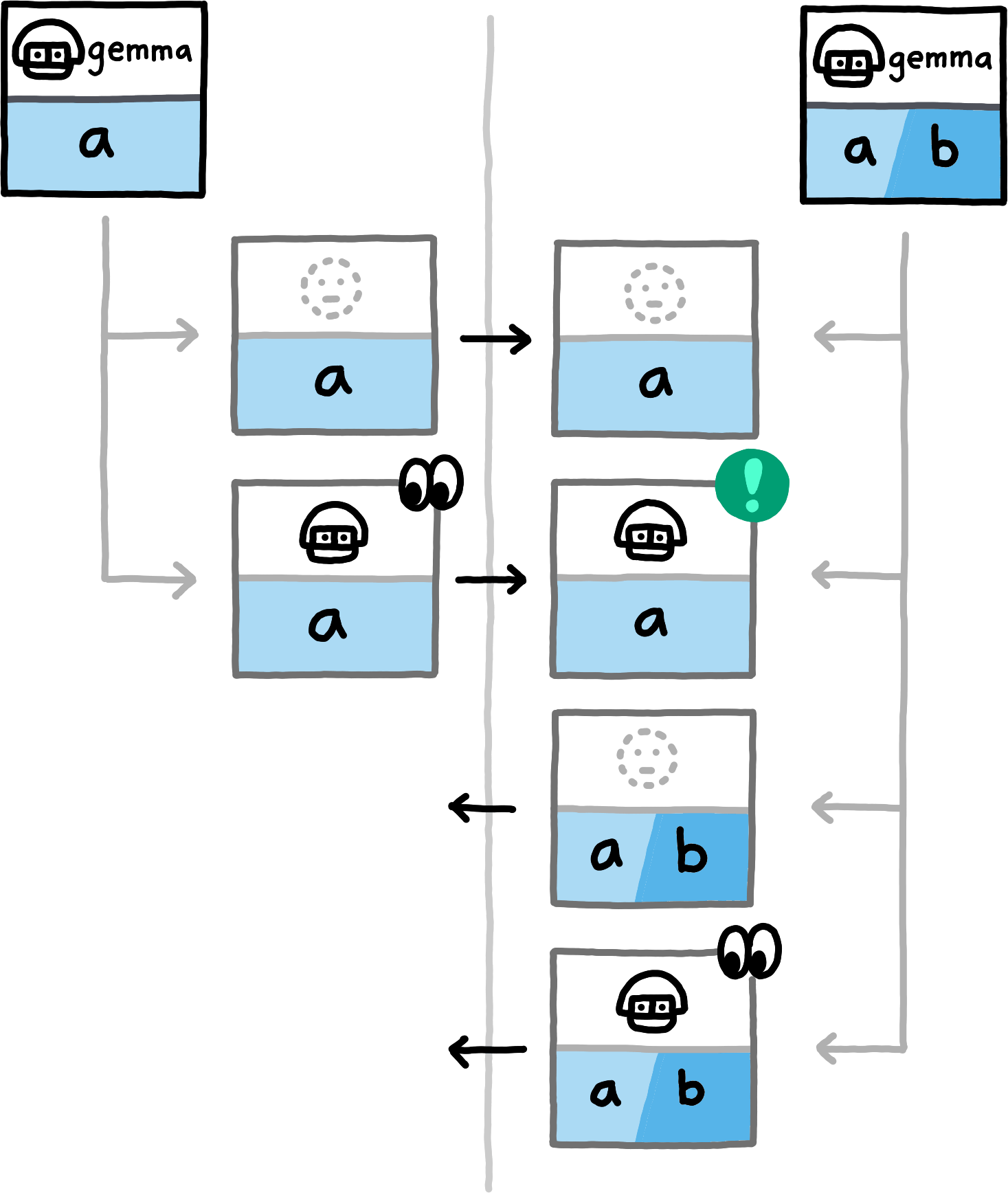
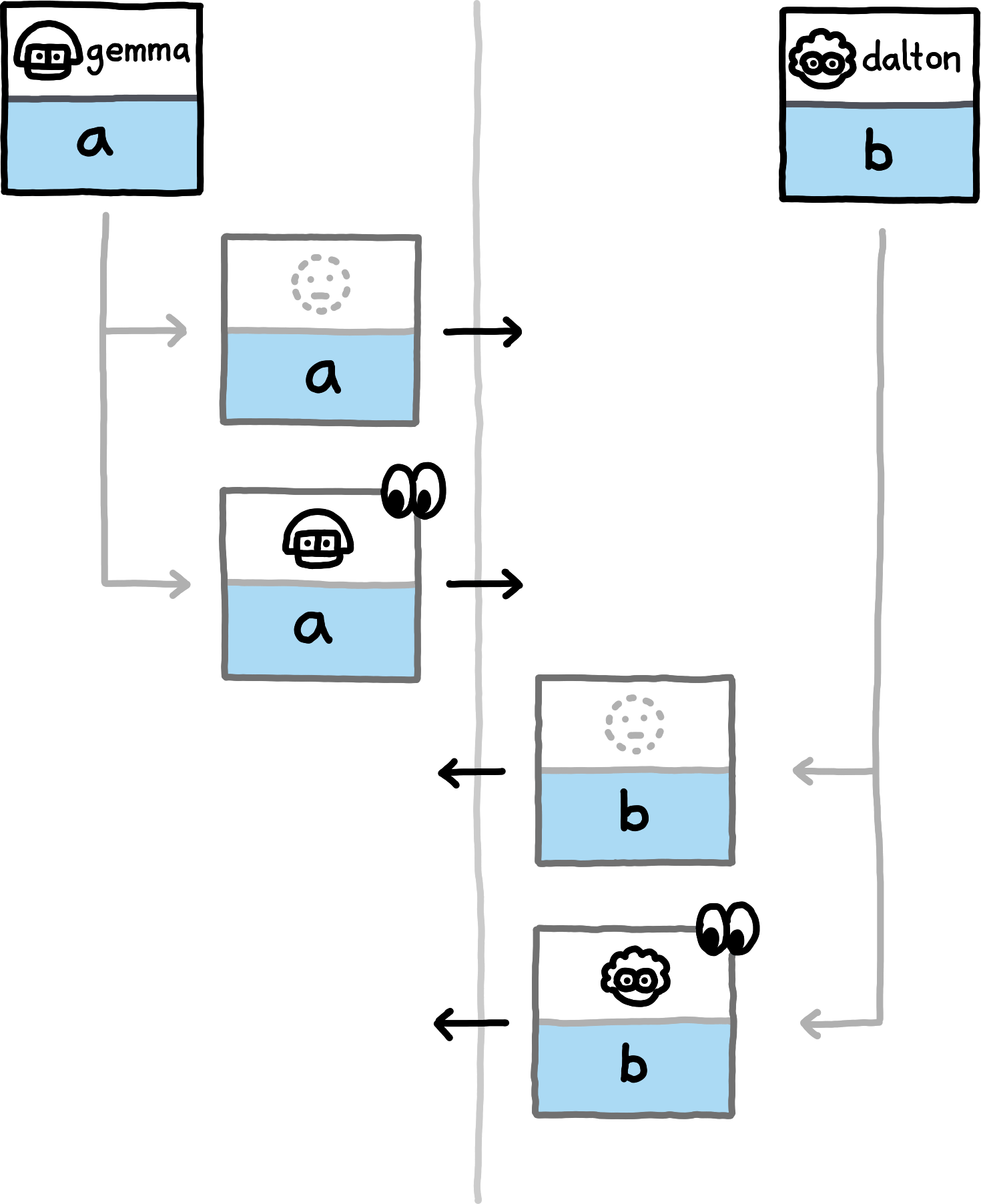
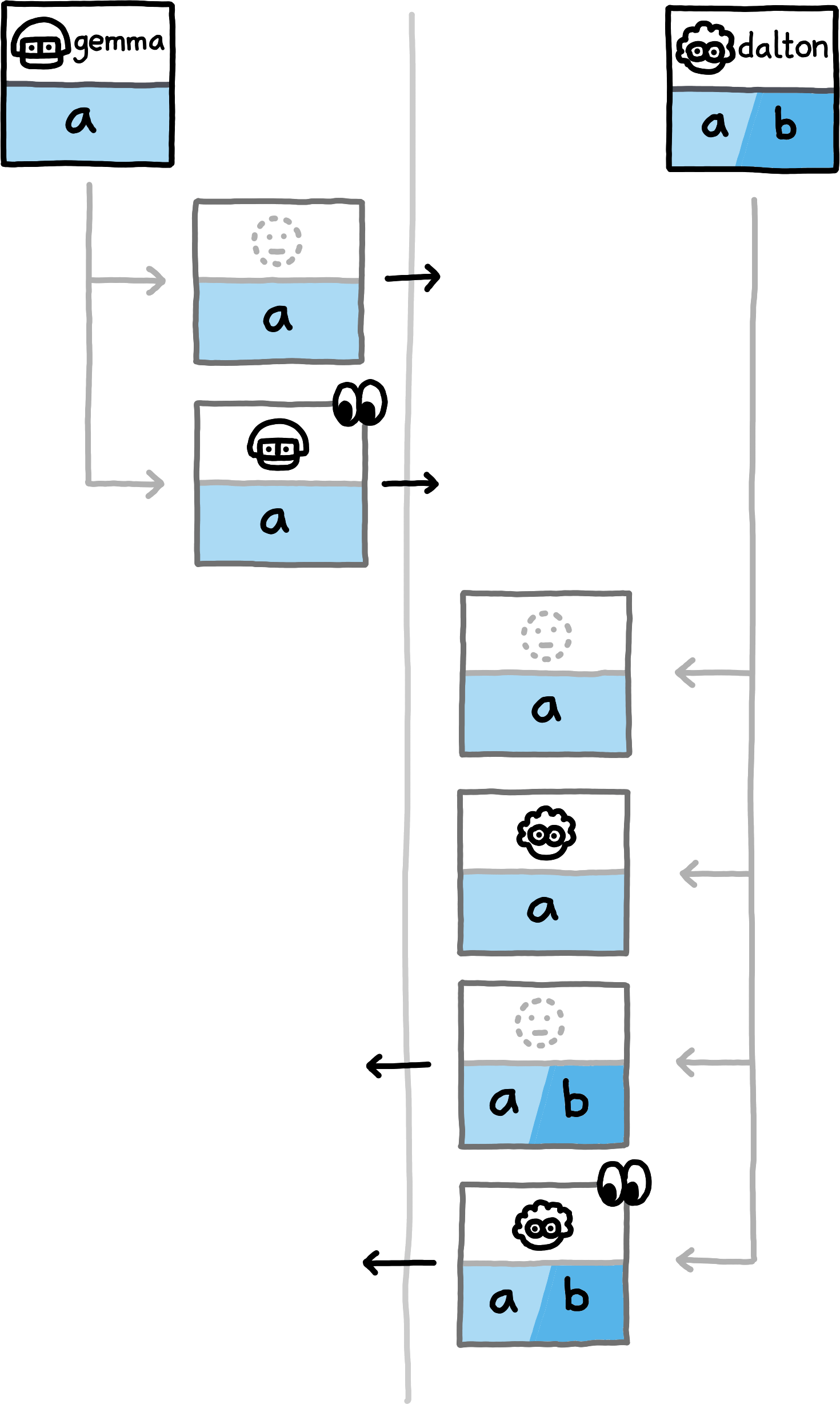
                          Left: Gemma subspace, path a
                          Right: Gemma subspace, path b
                          The PrivateInterests are disjoint. None of the hashes match.
                          Left: Gemma subspace, path a
                          Right: Gemma subspace, path ab
                          The PrivateInterests are not disjoint. The right peer detects an overlap.
                          Left: Gemma subspace, path a
                          Right: Dalton subspace, path b
                          The PrivateInterests are disjoint. None of the hashes match.
                          Left: Gemma subspace, path a
                          Right: Dalton subspace, path ab
                          The PrivateInterests are disjoint. The only matching hashes are both accompanied by a boolean of false.

                          Exchanging Capabilities

                          The previous scheme ensures that whenever two PrivateInterests submitted by different peers are not disjoint, one peer becomes aware of that fact. The next step is to let the peers exchange their corresponding read capabilities. This requires some care, however, since no information must be leaked if the other peer merely knew or guessed a PrivateInterest but does not have a read capability that certifies that the peer may learn information about corresponding Areas.

                          An example: Muriarty submits a PrivateInterest with path a, and Alfie detects an overlap with his PrivateInterest of path a (and the same namespace_ids and subspace_id). But Muriarty does not actually have a read capability for and Area with the path a. If Alfie simply transmitted his read capability first, then Muriarty would learn that b is a meaningful Path suffix in an Area in which he should not be able to learn anything.

                          In general, whenever there is an overlap in the two peer’s PrivateInterests, one of three situations occurs:

                          1. One of the PrivateInterests is strictly more specific than the other. The peer who has the more specific PrivateInterest is the one to detect the overlap. This peer sends an overlap announcement message to the other peer to announce the overlap, the other peer then sends its read capabilities which certify read access to Areas included in the less specific PrivateInterest.
                          2. Both PrivateInterests are equal. Both peers are able to detect this — the matching hashes correspond to a PrivateInterest with a path in which they are themselves directly interested in. Both peers can and should immediately send their read capabilities.
                          3. The two PrivateInterests are awkward. We discuss this case later and ignore it for now.

                          Upon receiving an overlap announcement, a peer sends its read capabilities whose granted areas are included in the PrivateInterests in question. Upon receiving such a read capability, a peer answers with its own intersecting read capabilities (if it hadn’t sent them for other reasons already).

                          The scheme of replying with sensitive information to overlap announcements is obviously broken if peers can simply claim an overlap for arbitrary hashes. But we can prevent this by mandating that every overlap announcement contains an announcement authentication in the form of the hash of the corresponding PrivateInterest salted with the announcer’s salt. So when the initiator announces an overlap, that overlap announcement must contain the hash salted with ini_salt, and overlap announcements by the responder must contain the hash salted with res_salt. These salted hashes can only be produced by somebody who actually knows the PrivateInterest in question.

                          Naively transmitting read capabilities would allow an active eavesdropper to learn the information in the capabilities. Hence, the transmission of the capabilities must omit all sensitive information. This is possible because the two peers a have a shared context — the less specific of the non-disjoint PrivateInterests — whose information can be omitted from the capability encoding. We provide a suitable encoding44Our encoding also includes the well-known receiver in the shared context, in the form of a PersonalPrivateInterest. This is simply an optimisation to shave off a few more bytes, not a critical security feature. Things work out quite nicely here: omitting the shared information not only secures confidentiality, but also means transmitting fewer bytes. for Meadowcap capabilities, users of different capability systems need to define their own encodings.

                          Note that peers need to store a potentially unbounded number of hash-boolean pairs that they receive, but they do not have an unbounded amount of memory. In Confidential Sync, we employ LCMUX and the notion of resource handles to deal with this problem. When resource limits are communicated and enforced, how should peers select which PrivateInterests they submit?

                          Imagine two peers, with the exact same 400 PrivateInterests, but they can each submit only 20 into the private overlap detection process due to resource limits. If they each selected 20 of their interests at random, they would likely part ways thinking they don't share any common interests. If they both sorted their PrivateInterests (say, lexicographically according to some agreed-upon encoding) and transmitted the first 20 ones, then observers might be able to reconstruct some information about their interests.

                          As a solution, both peers should send the PrivateInterests whose hashes, salted with ini_salt, are their numerically least hashes. This way, the sorting order is an independent, random permutation in each session, yet peers with large overlaps in their PrivateInterests are likely to detect that overlap.

                          Dealing With Awkwardness

                          The exchange of read capabilities that we have described so far works for pairs of PrivateInterests where one is more specific than the other. This is not the case for awkward pairs, however. The peer who detects the overlap cannot send its own read capability for the same reason as in all other cases: the Path is an extension of the Path that the other peer knows about, so it must not be transmitted blindly. But the other peer cannot send its read capability either, because it contains a SubspaceId that must not be disclosed blindly.

                          To resolve this standoff, we allow the peer who detected the overlap to prove that it is allowed to learn about arbitrary SubspaceIds that are in use in some namespace, without leaking any specific Paths. To this end, we introduce a separate kind of capability: the enumeration capability.

                          An enumeration capability is an unforgeable token with two types of semantics:

                          Whenever some entity is granted a read capability, it should also55This is not necessary if the read capability is of a form that makes it impossible to be part of an awkward pair. be granted an enumeration capability with the same receiver. When, during sync, a peer detects an awkward pair, it attaches to its overlap announcement its enumeration capability for the namespace in question, using an encoding that omits all sensitive information66We provide a Meadowcap-like capability type at the end of this document, and a suitable, confidentiality-preserving encoding here. (i.e., typically, the NamespaceId of the granted namespace). The other peer replies to the overlap announcement only if the receiver matches the ini_pk or the res_pk (depending on role) and the granted namespace matches the namespace_id of the PrivateInterest.

                          Since the announcer does not know the subspace_id of the other peer’s PrivateInterest in this case, the announcer cannot provide the correctly salted hash of the other’s PrivateInterest as a announcement authentication. For awkward pairs, the announcement authentication is thus the salted hash over the PrivateInterest that was submitted by the other peer, except its subspace_id is replaced with any.

                          Security Properties

                          We now lay out out the security model of this approach: which data gets exposed in which scenarios? We do not have formal proofs for any of these claims, these are merely our design goals (which we believe to have achieved).

                          Throughout the following, Alfie and Betty are honest peers, Muriarty is a malicious peer who may deviate arbitrarily from Confidential Sync, and Epson is an active eavesdropper on the networking layer who can read, modify, drop, or insert arbitrary bytes on a Confidential Sync communication channel.

                          Threat Model

                          We consider two primary scenarios:

                          • Alfie and Muriarty sync, and Muriarty tries to glean as much information from/about Alfie as possible.
                          • Alfie and Betty sync without knowing any long-term secrets of each other, and Epson attacks the session and tries to glean as much information from/about Alfie and Betty.

                          Note that Epson can simulate a Muriarty, or they could even be the same person. Epson is only interesting for cases where Alfie syncs with somebody who has more knowledge than Epson, so we do not consider the cases where Muriarty and Epson collaborate.

                          If Alfie and Betty know longterm public keys, they can exclude an active attacker during the handshake. If only one of them knows a longterm secret of the other, Epson is less powerful than in the setting where neither knows a longterm secret of the other; hence we only analyze the prior scenario.

                          Scope

                          We now list the information we wish to keep confidential. We group it in four levels, based on which kind of peer or attacker is allowed to glean which information.

                          L0
                          L1
                          L2
                          L3
                          • Fingerprintable session behaviour, such as resource control, error handling, etc. Virtually impossible to list exhaustively.

                          We consider fingerprinting, tracking, and deanonymisation based on information from L3 to be out of scope of this document.

                          Goals

                          We now describe which kind of information can be learned by which kind of attacker. A rough summary:

                          • With a valid read capability, you can access all corresponding information (L0 and below). This is a feature.
                          • If you know or guess a PrivateInterest without holding a corresponding read capability, you can access information at L1 and below.
                          • An active eavesdropper can access everything at L2 without holding a corresponding read capability.

                          Consequently, NamespaceIds, SubspaceIds, and Paths that cannot be guessed are never leaked by using Confidential Sync. Conversely, attackers can confirm their guesses about PrivateInterests to some degree. Hence, it is important to keep NamespaceIds, SubspaceIds, and Paths unguessable by introducing sufficient entropy.

                          Syncing with Muriarty

                          When Alfie syncs with a malicious peer Muriarty, Muriarty is able to glean the following information:

                          Syncing Attacked By Epson

                          If Alfie syncs with an honest peer Betty, but an active attacker Epson can read and manipulate the communication channel, that attacker can glean the following information:

                          Meadowcap Enumeration Capabilities

                          We conclude by presenting a datatype that implements enumeration capabilities, nicely complementing Meadowcap. Note that in Meadowcap, read capabilities for all subspaces of a namespace can only exist in owned namespaces.

                          A capability that certifies read access to arbitrary SubspaceIds at some unspecified Path.
                           
                          The namespace for which this grants access.
                           
                          The user to whom this initially grants access (the starting point for any further delegations).
                           
                          Authorisation of the user_key by the namespace_key.
                           
                          Successive authorisations of new UserPublicKeys.
                          }

                          The receiver of a McEnumerationCapability is the final UserPublicKey in the delegations, or the user_key if the delegations are empty.

                          The granted namespace of a McEnumerationCapability is its namespace_key.

                          Validity governs how McEnumerationCapabilities can be delegated. We define validity based on the number of delegations:

                          A McEnumerationCapability with zero delegations is valid if initial_authorisation is a NamespaceSignature issued by the namespace_key over the byte 0x04, followed by the user_key (encoded via encode_user_pk).

                          For a McEnumerationCapabilities cap with more than zero delegations, let (new_user, new_signature) be the final pair of cap.delegations, and let prev_cap be the McEnumerationCapability obtained by removing the last pair from cap.delegations. Denote the receiver of prev_cap as prev_receiver.

                          Then cap is valid if prev_cap is valid, and new_signature is a UserSignature issued by the prev_receiver over the bytestring handover, which is defined as follows:

                          References